Diagonal principal de una matriz

La diagonal principal de una matriz cuadrada es una línea recta imaginaria que empieza por el extremo superior izquierdo a₁₁ y acaba en el extremo inferior derecho de la matriz a_nn

En este post debes estar muy atento a las preguntas que te voy a realizar, sabes que existe la diagonal principal y secundaria de una matriz.

Que puedes identificar la diagonal principal de una matriz 4×3 o no cuadrada. Esto y mucho más en este post. Vamos a por ello

¿Qué quiere decir diagonal principal?

¿Cuál es la diagonal principal de una matriz? buena pregunta, antes de nada decirte que se refiere a matrices cuadradas, entonces cuál es la definición de diagonal, si te hablo de la diagonal principal me estoy refiriendo a una recta imaginaria que va desde el extremo superior izquierdo hasta el extremo inferior derecho de la matriz.

Como puedes ver en esta diagonal ejemplo, trazo una línea imaginaria desde el extremo superior izquierdo (2) y el extremo inferior derecho (1).

Entonces ¿Qué matrices tienen diagonal principal? pues la matrices cuadradas.

Elementos de la diagonal principal de una matriz

Otra forma de definirla es considerar los elementos de la matriz cuadrada que tengan asignado el mismo número de fila que de columna, por ejemplo lo puedes ver en esta matriz de orden 4.

Como podéis observar he señalado aquellos elementos que pertenecen a la diagonal principal y como resultado puedes observar que tiene el mismo número de fila que de columna como puedes observar en la imagen.

Es decir, todos los elementos que tengan fila y columna igual forman parte de la diagonal principal, como resultado en este ejemplo tenemos a₁₁ =1;a₂₂ =1;a₃₃ =-1;a₄₄ =3.

Representación de la diagonal de una matriz cuadrada de orden n

Has visto dos conceptos de cómo identificarla, y ahora te voy a dar la definición general. Si observas en la imagen tenemos una matriz de orden n, y los elementos de la matriz que están en verde son los que pertenecen a la diagonal.

Existe otra que es la llamada diagonal secundaria de una matriz, la verdad que no tiene mucho interés pero la que de verdad tiene interés es la diagonal principal de una matriz cuadrada. Vamos a ver qué características tiene.

Están siendo muchos datos sobre matrices, si te encuentras un poco perdido te recomiendo que veas las propiedades de las matrices

¡Descubre las matemáticas en nuestro canal de YouTube! 🌟 Aprende trucos, resuelve problemas paso a paso y domina conceptos clave con nuestros vídeos fáciles de seguir. 🚀 Haz clic aquí y empieza a disfrutar de las matemáticas de forma sencilla y divertida. ¡Te esperamos! 🎓📚

Propiedades

La diagonal principal no solo es útil para la notación y el manejo de matrices, sino que también posee propiedades especiales que son cruciales en diversas áreas de la matemática y sus aplicaciones:

1. Determinante: El determinante de una matriz triangular (ya sea superior o inferior) es el producto de los elementos de su diagonal principal.
2. Trazas: La traza de una matriz es la suma de los elementos de su diagonal principal. Esta propiedad es particularmente útil en la teoría de matrices y en el cálculo de transformaciones lineales.
3. Ortogonalidad: En matrices ortogonales, los elementos de la diagonal principal están relacionados con las propiedades de las transformaciones que conservan longitudes y ángulos.

Como especialista en matrices, siempre he encontrado que entender estas propiedades es fundamental para enseñar a los estudiantes cómo manejar problemas más complejos en el álgebra lineal.

Ejercicios y Problemas Resueltos sobre Diagonales Principales

A lo largo de mi carrera, he desarrollado numerosos ejercicios para ayudar a los estudiantes a dominar este concepto. Aquí comparto algunos problemas resueltos que considero fundamentales para entender a fondo la diagonal principal.

Problema 1: Identificación y Cálculo de la Traza

Dada la matriz:

Identifica los elementos de la diagonal principal y calcula la traza.

Solución: Los elementos de la diagonal principal son 3, 5 y 5. La traza de D es 3+5+5=3 + 5 + 5 =13.

Problema 2: Determinante de una Matriz Triangular

Dada la matriz triangular inferior:

Calcula el determinante.

Solución: El determinante de una matriz triangular es el producto de los elementos de su diagonal principal: 2×1×6=12.

¿Cómo calcular la diagonal secundaria de una matriz?

Ya tienes claro ¿cuáles son los elementos de la diagonal principal?, sí, pues te comento que existen dos diagonales y cuando leas o te digan qué son las diagonales, estarán en lo cierto, pero ¿qué es la diagonal secundaria de una matriz? ¿cómo se llama?

¿Qué es la diagonal principal y secundaria? la diagonal principal y secundaria de una matriz cuadrada, aunque es la principal la que tiene mucho más valor matemático que la secundaria, bueno, la diagonal secundaria de una matriz son todos aquellos elementos que van desde la esquina superior derecha hasta la esquina inferior izquierda.

Pero esta no es la diagonal de la matriz más importante.

Observa que los elementos que pertenecen a la diagonal secundaria son a₁₄ =0;a₂₃ =3;a₃₂ =0;a₄₁ =-1; y tienen una característica en común, fíjate. Si sumas la fila y la columna correspondiente todas suman 5, que es lo mismo que el orden de la matriz, 4, más 1, es decir, 5.

De forma general, cómo calcular la diagonal secundaria de una matriz… pues de esta forma.

Una vez que tienes clara la definición su significado o concepto diagonal puedes ver las aplicaciones que tiene en otras matrices, por ejemplo qué es una matriz diagonal u otro tipo de matriz cuadrada relacionada con la diagonal principal de una matriz, como las matrices triangulares superiores o inferiores.

Entonces si ya lo tienes claro ¿cuántas diagonales tiene una matriz de 3×3 o cuál es la diagonal principal de una matriz 3×4? la respuesta ya es fácil, la principal, que es la más importante, y la secundaria.

¿Existe la diagonal principal de una matriz rectangular?

Si atendemos a la definición que hemos dado podemos decir que la diagonal principal de una matriz no cuadrada no existe como tal. Sí, nos podemos acercar de esta forma, mira este ejemplo de la diagonal principal de una matriz 4×3

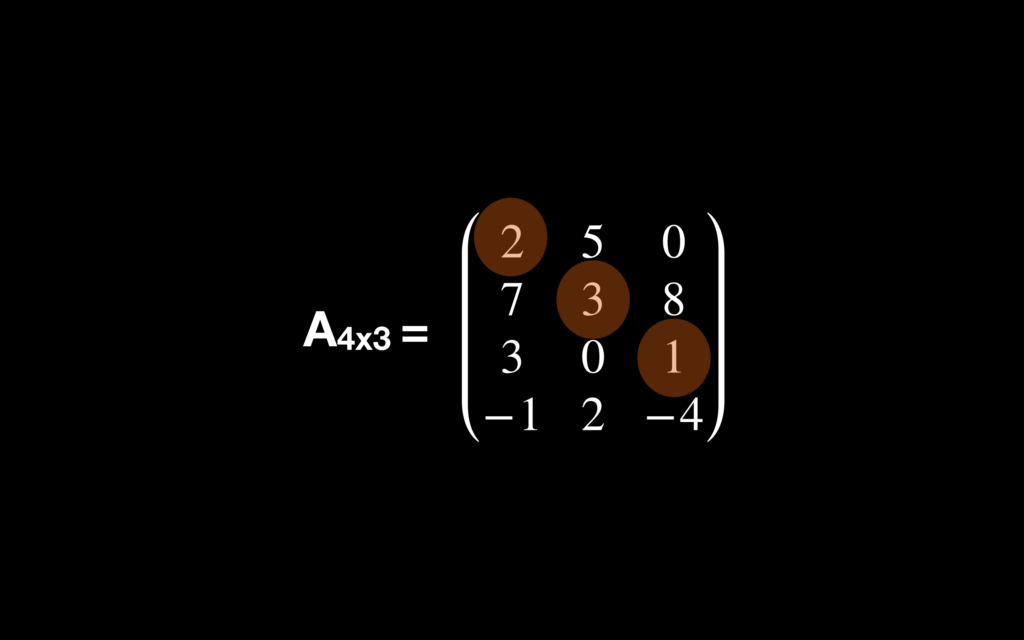
Aplicaciones de la Diagonal Principal en la Matemática

La diagonal principal tiene aplicaciones que van más allá de la teoría pura y se extienden a varios campos prácticos. En mi experiencia, la conexión de la teoría de matrices con aplicaciones reales puede motivar a los estudiantes y profesionales a profundizar en su estudio.

Aplicaciones en Ciencias de la Computación

Los algoritmos de optimización y las redes neuronales a menudo utilizan matrices, y comprender la diagonal principal es crucial para implementar y mejorar estos algoritmos.

Aplicaciones en Economía

En econometría y modelos económicos, las matrices y sus diagonales principales son utilizadas para representar y resolver sistemas de ecuaciones simultáneas, cruciales para el análisis económico.

Aplicaciones en Física

La diagonalización de matrices es una herramienta clave en la mecánica cuántica y otros campos de la física, donde se requiere simplificar matrices complejas para encontrar soluciones de sistemas físicos.

Conclusiones y Reflexiones Finales

Entender la diagonal principal de una matriz no solo es fundamental para los estudios matemáticos avanzados, sino que también tiene aplicaciones prácticas que abarcan múltiples disciplinas. Como profesor de matemáticas con más de tres décadas de experiencia, he visto cómo este conocimiento puede transformar la comprensión de los estudiantes y su capacidad para resolver problemas complejos.

Espero que este artículo haya proporcionado una visión completa y práctica de la diagonal principal de una matriz. Con un enfoque en ejemplos prácticos, aplicaciones teóricas y la integración de mi experiencia personal, busco ofrecer una guía útil y accesible para todos aquellos interesados en profundizar en el fascinante mundo de las matrices.

TE PUEDE INTERESAR:

ANÁLISIS MATEMÁTICO