5+8 PROPIEDADES DE LAS DERIVADAS Tablas Pdf

Propiedades de las derivadas. Aprende a ¿cómo derivar funciones? aplicando las propiedades de derivadas:

Derivada de la suma

Derivada del resto

Derivada de una multiplicación de funciones

Derivada de la división de funciones

Sin más EMPEZAMOS

Contenidos que vas a ver

Imágenes que necesitas de la derivada

Soy Pepe, profesor de matemáticas y ciencias en general, con más de 25 años de experiencia, toda la información que vas a recibir es veraz y te ayudará a entender mejor. ¡Sigue leyendo!

Sabiendo que la derivada de una función en un número o constante es la tasa de variación de la función al variar el número de forma infinitesimal, se han creado unas reglas de derivación. Geométricamente hablando se relaciona con la recta tangente y con los límites también.

En este apartado te daré unas tablas que te van a ayudar a entender las reglas de las derivadas, en otras palabras, sabrás cómo utilizar la tabla de derivadas para derivar y un acercamiento a las propiedades de derivación. Aquí tienes una galería de imágenes sobre tablas de derivadas

tabla de derivadas inmediatas, reglas de derivacioncalculo de derivadasderivadas reglasformula de la derivadafórmula de la derivadapropiedades de la derivadaderivadas propiedadespropiedades de derivadapropiedades derivadaspropiedades de derivadas — Tabla de derivadas inmediatas

tabla de derivadas compuesta, reglas de derivacioncalculo de derivadasderivadas reglasformula de la derivadafórmula de la derivadapropiedades de la derivadaderivadas propiedadespropiedades de derivadapropiedades derivadaspropiedades de derivadas — Tabla de derivadas inmediatas

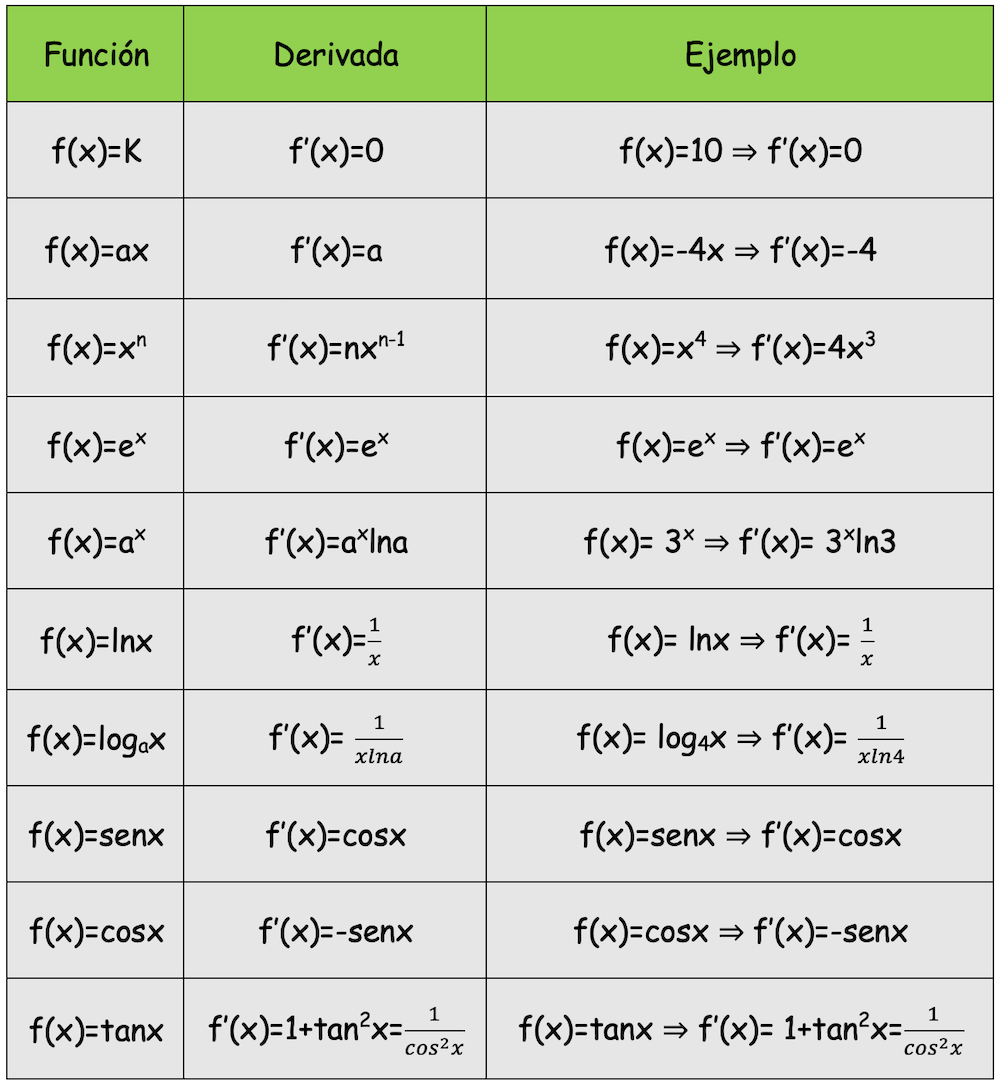
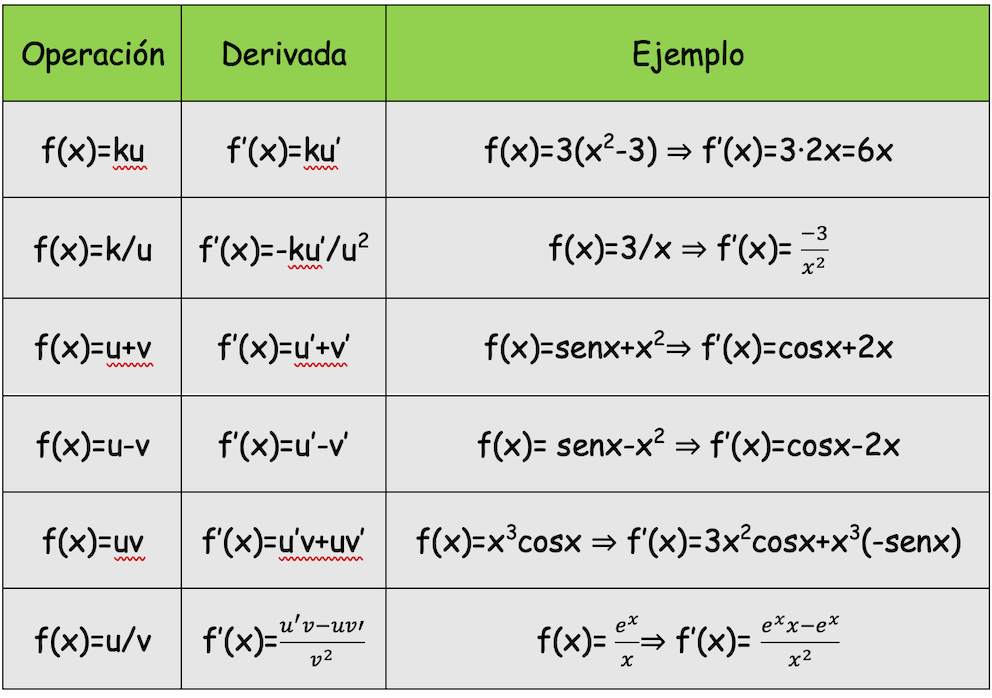
Tabla de derivadas de funciones trigonométricas

Aquí tienes los distintos tipos de derivadas trigonométricas. Las siguientes funciones de ejemplo tienen, algunas, el ángulo elevado al cuadrado y otras es la función la que está elevada al cuadrado.

Tabla de derivada trigonométrica

Propiedades de las derivada ¿Cómo se llaman las 5 reglas para derivar?

Estas son las 5 primeras propiedades del álgebra de derivadas de funciones reales de variable real, lo más importante, caen en el olvido pero si las aplicas, la derivada, en muchos casos, son fáciles.

Consideremos que f(x), g(x), u y v son funciones y que k es una constante. Aquí tienes las leyes de derivadas que te ayudará a calcular cualquier derivada. Por ejemplo, la derivada de la suma de funciones te ayuda a derivar una función polinómica.

Derivada de una constante

Esta es la regla para derivar f(x)=k → f'(x)=0, la derivada es igual a cero.

Derivada de la suma de funciones

En primer lugar, las propiedades básicas de las derivadas de una suma de funciones es igual a la suma de las derivadas de cada una de las funciones por separado.

Calcular la derivada de f(x)=u+v ➪ f'(x)=u’+v’

Derivada de una resta de funciones

En segundo lugar, esta propiedad de la derivada de una resta de funciones es igual a la resta de las derivadas de cada una de las funciones por separado.

f(x)=u–v ➪ f'(x)=u’-v’

Derivada del producto de funciones

Esta propiedad de función derivable te va a proporcionar una herramienta matemática para calcular multitud de ejercicios de forma más simple. Además, la derivada del producto de dos funciones es igual a la derivada de la primera función por la segunda sin derivar, más la primera sin derivar por la segunda derivada.

Regla del producto f(x)=u·v ➪ f'(x)=u’·v+u·v’

Derivada del cociente de funciones

A continuación, la derivada de una división de dos funciones, esta propiedad es igual al cociente de la derivada de la función numerador por la función del denominador sin derivar, menos la función del numerador sin derivar por la del denominador derivada entre la función del denominador al cuadrado

f(x)=u/v ➪ f'(x)=(u’·vu·v’)/v ²

Regla de la cadena

Y además esta propiedad, la regla de la cadena: sean f(x), u y v tres funciones reales de variable real, de modo que f(x)=(u∘v)(x)=u(v(x)). La fórmula que nos dará f'(x) es (u∘v)'(x)=u'(v(x))·v'(x), esta regla te sirve para funciones compuestas.

¡¡¡ATENCIÓN!!!

Tratando este tema te recomiendo que no olvides que las normas de derivación que estás viendo por sí solas, no te va a servir para mejorar tus conocimientos sobre la teoría de las derivadas ¡CLICLA!

¿Cuáles son las 8 reglas de derivación de funciones?

Qué son derivadas. Aquí te voy a proporcionar tres reglas más de derivación que sin duda, te van a ayudar bastante en algunos casos que veremos en los ejercicios que haremos más adelante. Consideremos que f(x), g(x), u y v son funciones y que k es una constante, función en otras palabras.

En primer lugar, la derivada de una suma de funciones es igual a la suma de las derivadas de cada una de las funciones por separado. Aquí tienes la fórmula de la suma de funciones.

f(x)=u+v ➪ f'(x)=u’+v’

En segundo lugar, la derivada de una resta de funciones es igual a la resta de las derivadas de cada una de las funciones por separado.

f(x)=uv ➪ f'(x)=u’-v’

Además, la derivada del producto de una constante k por una función es igual a la constante multiplicada por la derivada de la función, debido a que la derivada de una constante es cero, una constante puede ser cualquier número real o carácter. Propiedades de las derivadas multiplicación

f(x)=k·u ➪ f'(x)=k·u’

En cuarto lugar, la derivada de una multiplicación o producto de dos funciones es igual a la derivada de la primera función por la segunda sin derivar, más la primera sin derivar por la segunda derivada.

f(x)=u·v ➪ f'(x)=u’·v+u·v’

A continuación, cómo se hacen las derivadas de una división de una constante k entre una función es igual al cociente de menos la constante k por la derivada de la función del denominador entre la función del denominador al cuadrado.

f(x)=k/v ➪ f'(x)=(-k·v’)/v²

La derivada de una división de funciones es igual al cociente de la derivada de la función numerador por la función del denominador sin derivar, menos la función del numerador sin derivar por la del denominador derivada entre la función del denominador al cuadrado

f(x)=u/v ➪ f'(x)=(u’·v-u·v’)/v²

Y además, resolver derivadas de funciones con la regla de la cadena: sean f(x), u y v tres funciones reales de variable real, de modo que f(x)=(u∘v)(x)=u(v(x)). La fórmula que nos dará f'(x) es (u∘v)'(x)=u'(v(x))·v'(x), como por ejemplo la derivada de arcoseno

Y por último, derivación de la inversa de una función: sea f una función real de variable real que tiene función inversa f^-1(x), la derivada de la función inversa de f(x) es:
(f^-1)'(x)=1/f'(f^-1(x))

Todas estas fórmulas de derivadas están en forma de tablas. Pero, no podrás ver la raíz cuadrada derivada, esto está en otra web sobre tabla de derivadas.

Esquema de las Propiedades de las derivadas inmediatas con ejemplos

Y después de eso te voy a aplicar estas propiedades de las derivadas inmediatas para que veas cómo se hacen los ejercicios para que aprendas fácilmente a tu ritmo. Ten en cuenta que u’ y v’ son la derivada de una función cualquiera. Cuidado con la fórmula de división derivadas.

Aquí tienes las reglas de las derivadas ejemplos. Alguna de ellas tienen potencia, ten cuidado. Aquí tienes las funciones derivables en forma de tabla.

Propiedades de las derivadas fórmulas	Ejercicio
f(x)=u+v ➪ f'(x)=u’+v’	f(x)=x²+1/x ➪ f'(x)=2x-(1/x²)
f(x)=u-v ➪ f'(x)=u’-v’, resta de derivadas	f(x)=4x-(2x-1)² ➪ f'(x)=4-2(2x-1)·2
f(x)=k·u ➪ f'(x)=k·u’	f(x)=8x² ➪ f'(x)=8·2x=16x
f(x)=u·v ➪ f'(x)=u’·v+u·v’	f(x)=x²·(3x²-3)➪ f'(x)=2x·(3x²-3)+x²·6x
f(x)=k/v ➪ f'(x)=(-k·v’)/v²	f(x)=4/x ➪ f'(x)=(-4·2x/x²)=-8/x
f(x)=u/v ➪ f'(x)=(u’·v-u·v’)/v²	f(x)=(2x-1)/x ➪ f'(x)=(2·x-(2x-1)·1)/x²=1/x²

Propiedades de las derivadas trigonométricas

Del mismo modo, en este caso te voy a resolver ejercicios de derivadas trigonométricas. En formato tabla.

Tabla propiedades de las derivadas ejemplos. La función de cada ejemplo, es una función derivable

Propiedades de las derivadas fórmulas	Ejercicio
f(x)=u+v ➪ f'(x)=u’+v’	f(x)=senx+cosx ➪ f'(x)=cosx+(-senx)
f(x)=u-v ➪ f'(x)=u’-v’, resta de derivadas	f(x)=tgx-cosx ➪ f'(x)=1+tg²x-(-senx)
f(x)=k·u ➪ f'(x)=k·u’	f(x)=8cotgx ➪ f'(x)=8·(-(1+cotg² x))
f(x)=u·v ➪ f'(x)=u’·v+u·v’	f(x)=senx·cosx➪ f'(x)=cosx·cosx+senx·(-senx)
f(x)=k/v ➪ f'(x)=(-k·v’)/v²	f(x)=4/cosx ➪ f'(x)=(-4·(-senx)/cos²x)=
f(x)=u/v ➪ f'(x)=(u’·v-u·v’)/v²	f(x)=senx/cosx ➪ f'(x)=(cosx·cosx-senx·(-senx))/cos²x=1/cos²x

Propiedades de las derivadas logarítmicas

Lo que voy a resolver es alguna derivada de los logaritmos tanto neperianos como de base distinta de e aplicando las reglas de derivación.

Propiedades de las derivadas fórmulas	Ejercicio
f(x)=u+v ➪ f'(x)=u’+v’	f(x)=x²+lnx ➪ f'(x)=2x+(1/x)
f(x)=u-v ➪ f'(x)=u’-v’	f(x)=4x-log₂ x ➪ f'(x)=4-1/(xln2)
f(x)=k·u ➪ f'(x)=k·u’	f(x)=8ln(2x-1) ➪ f'(x)=8·(2/(2x-1))
f(x)=u·v ➪ f'(x)=u’·v+u·v’	f(x)=lnx·log₃ (3x²-3)➪ f'(x)=(1/x)·log₃ (3x²-3)+lnx·(6x/(3x²-3)ln3
f(x)=k/v ➪ f'(x)=(-k·v’)/v²	f(x)=4/lnx ➪ f'(x)=(-4·(1/x)/ln²x)=-4/(x·ln²x)
f(x)=u/v ➪ f'(x)=(u’·v-u·v’)/v²	f(x)=(2x-1)/lnx ➪ f'(x)=(2·lnx-2x·(1/x))/ln²x=2·(lnx-1))/ln²x

Propiedades de las derivadas exponenciales

Y ahora a continuación, tocan las funciones exponenciales, seguiré con las misma pauta para que te ayude a mejorar a resolver la derivada.

Propiedades de las derivadas fórmulas	Ejercicio
f(x)=u+v ➪ f'(x)=u’+v’	f(x)=2^x+e^x ➪ f'(x)=2^xln2+e^x
f(x)=u-v ➪ f'(x)=u’-v’	f(x)=4^2x-e^2x ➪ f'(x)=2·4^2xln4-2e^2x
f(x)=k·u ➪ f'(x)=k·u’	f(x)=8e^2x ➪ f'(x)=8·2·e^2x=16e^2x
f(x)=u·v ➪ f'(x)=u’·v+u·v’	f(x)=x²·e^2x➪ f'(x)=2x·e^2x+x²·2·e^2x
f(x)=k/v ➪ f'(x)=(-k·v’)/v²	f(x)=4/5^2x ➪ f'(x)=(-4·2·5^2xln5/5^4x)=(-8·ln5/5^2x)
f(x)=u/v ➪ f'(x)=(u’·v-u·v’)/v²	f(x)=(2x-1)/e^x ➪ f'(x)=(2·e^x-(2x-1)·e^x)/ e^2x= e^x·(2-2x+1))/ e^2x=(3-2x)/ e^x

Si te has preguntado cómo se haría una derivada segunda, pues no es más que derivar de nuevo la primera derivada. Sin más. La segunda derivada se suele utilizar para calcular máximos y mínimos y también el estudio de la concavidad y la convexidad de funciones.

Propiedades de las derivadas pdf

Por otro lado, aquí te dejo las reglas y propiedades para derivar funciones en pdf para que las imprimas. Propiedades de las derivadas o reglas de las derivadas pdf

Son fórmulas de derivadas pdf, junto con un ejemplo.

Qué son las derivadas

Te permite comprender:

El comportamiento de las funciones.
Sus características.
Estudiar cómo es la gráfica de una función.
La variación de la función respecto a la variación de la variable independiente.
Además de calcular su derivada.

Vídeos que te ayudarán a resolver todas las 7 propiedades de las derivadas

¿Cómo derivar una función? o ¿cómo resolver derivadas? cuando tienes que calcular la derivada de una función. El teorema de Rolle, derivabilidad y continuidad, productos y cocientes, la definición de derivadas gracias al límite para derivar, cálculo de derivadas, distintas derivadas de funciones, y muchos ejercicios más.

Los vídeos que te proporciono aquí te van a ayudar a resolver multitud de ejercicios de derivadas y además explicados paso a paso. Propiedades de las derivadas ejercicios resueltos incluso con potencia en las funciones.

propiedades de las derivadas, vídeo de ejercicios de propiedades de derivación, reglas de derivacioncalculo de derivadasderivadas reglasformula de la derivadafórmula de la derivadapropiedades de la derivadaderivadas propiedadespropiedades de derivadapropiedades derivadaspropiedades de derivadas, primera función, función derivada, funciones derivables, derivables en \, derivable en \, función constante, funciones es igual, segunda función, reglas de derivación, funciones trigonométricas.

¿Quieres resolver de forma correcta las derivadas de funciones aplicando las propiedades de las derivadas? Aquí tienes la solución a tus problemas, sobre todo, a partir del minuto 55 tienes ejercicios explicados paso a paso. Cómo hacer derivadas

Si eres como la gran mayoría de mis alumnos/as que tienen problemas a la hora de aplicar bien las reglas de derivación, no te sientas mal, no eres el único o la única. Lo más importante, aquí te doy la solución perfecta a tus problemas. Qué son las derivadas

propiedades y reglas de la derivación de funciones reales de varible real. Vídeo explicativo sobre cómo derivar, reglas de derivacioncalculo de derivadasderivadas reglasformula de la derivadafórmula de la derivadapropiedades de la derivadaderivadas propiedadespropiedades de derivadapropiedades derivadaspropiedades de derivadas, primera función, función derivada, funciones derivables, derivables en \, derivable en \, función constante, funciones es igual, segunda función, reglas de derivación, funciones trigonométricas.

Calculadora de derivadas

Voy a darte referencias de páginas para que veas dónde puedes calcular derivadas y comprobar que las estás calculando de forma correcta.

Calculadora de derivadas: esta página te proporciona la posibilidad resolver derivadas, de encontrar el resultado de la derivada, te da el desarrollo por pasos. Puedes calcular derivadas tanto las primeras, segundas…hasta la de quinto orden. Te da la posibilidad de hacer gráficas y además son interactivas. Lo único que no me gusta de este solucionador de derivadas es la interfaz para poder poner la derivada, no me gustan mucho los botones.

Symbolad derivadas: esta calculadora de derivadas de funciones te da la opción a encontrar tanto la solución como los pasos a seguir, tiene unos botones interactivos que te van a ayudar mucho a la hora de escribir las derivadas. Las soluciones son bastante claras y te aporta la gráfica de la función a integrar. Puedes hacer derivadas de distinto orden, en un punto en concreto, implícita incluso por definición.
Solumaths: página sencilla, eficaz, te da la solución y te resume los pasos a seguir, bastante resumido para mi gusto.