Racionalizar 🤔 ¿Qué Es La Racionalización Y Ejemplos?

Racionalizar…Un radical en el denominador, ¡¡¡AAAAAAAH!!! qué tengo que hacer.

Si eres de los que están perdidos y necesitan ayuda como en el chico de la foto…ESTÁS EN EL SITIO IDÓNEO.

Aquí encontrarás respuesta a preguntas como, ¿cómo hacer ejercicios de racionalización? ¿qué es racionalizar y un ejemplo, por favor?

VAMOS A COMENZAR

Contenidos que vas a ver

¿QUÉ ES RACIONALIZAR?

La racionalización de radicales consiste en:

Tener un radical, con cualquier índice, en el denominador de una fracción.
Eliminar todo radical que aparezca en el denominador.

La verdadera definición es el apartado 2 anterior…Pero ¡¡¡CÓMO!!!

Tienes que tener en cuenta que vas a utilizar las fracciones equivalentes, es decir, transformar la fracción inicial a otra equivalente donde no aparezca el radical, o los radicales, en el denominador.

Si quieres saber más sobre el conjunto de los números reales, solo tienes que querer informarte aquí

Ya Pepe, pero CÓMO…Vamos a verlo ya.

TIPOS DE RACIONALIZACIÓN

Los casos más frecuentes que te vas a encontrar son los siguientes:

Denominador con una sola raíz. El radical que te vas a encontrar puede ser de cualquier índice.
Denominador con una suma o diferencia. La suma o diferencia va a ser de dos términos y al menos uno de ellos debe ser un radical de orden 2.
Denominador con una suma o diferencia. La suma o diferencia va a ser de dos términos y al menos uno de ellos debe ser un radical de orden 3.

Este último caso es menos usual, pero sí es cierto, que más complicado. Vas a ver ejemplos de cada uno de los tipos de racionalización.

Primer caso de racionalización. ¿Cómo racionalizar 3 /√ 5?

Para conseguir una fracción equivalente a la dada debes multiplicar y dividir por una misma expresión…¿Y cuál va a ser esa expresión con la raíces cuadradas? Pues mira, debes multiplicar y dividir por el mismo radical que aparece en el denominador:

$\dpi{120} \large \frac{3}{\sqrt{5}}=\frac{3\cdot \sqrt{5}}{\sqrt{5}\cdot \sqrt{5}}=\frac{3\sqrt{5}}{\left ( ^{\sqrt{5}} \right )^2}=\frac{3\sqrt{5}}{5}$

¿Cómo racionalizar 2 /√ 5?

Otro ejemplo de racionalización parecido:

$\dpi{120} \large \frac{2}{\sqrt{5}}=\frac{2\cdot \sqrt{5}}{\sqrt{5}\cdot \sqrt{5}}=\frac{2\sqrt{5}}{\left ( ^{\sqrt{5}} \right )^2}=\frac{2\sqrt{5}}{5}$

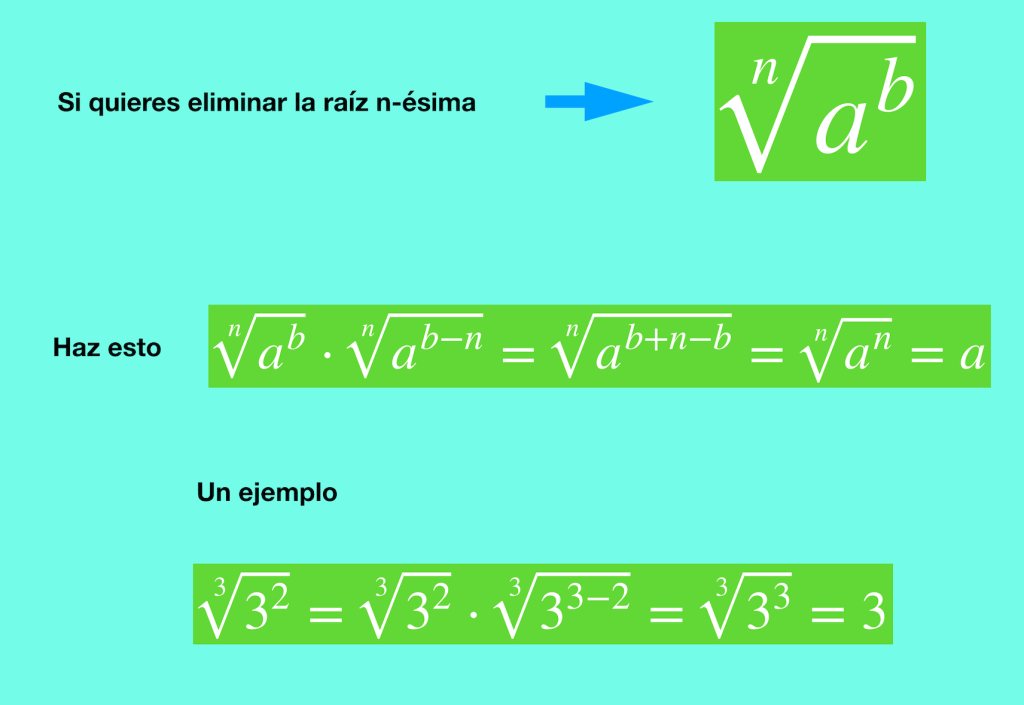
Cuando el radical no es cuadrado.

En este caso también se multiplica y se divide por una expresión, fíjate:

¿Te ayudo a racionalizar sumas y restas en el denominador?

En primer lugar

Conjugado de una raíz

El conjugado de una expresión que tiene radicales es aquel que hace que al multiplicar ambas expresiones desaparezcan los radicales.

Primer ejemplo:

Cuando en el denominador hay una suma y uno de los sumandos es una raíz cuadrada. (También vale si en el denominador aparece una resta de dos términos)

El conjugado solo es cambiar el signo a la expresión:

b+√c su conjugado es b-√c

FÍJATE QUE SE MULTIPLICA EL NUMERADOR Y EL DENOMINADOR POR EL CONJUGADO. EN CASO CONTRARIO ESTARÍA MAL

AQUÍ TIENES UN EJEMPLO

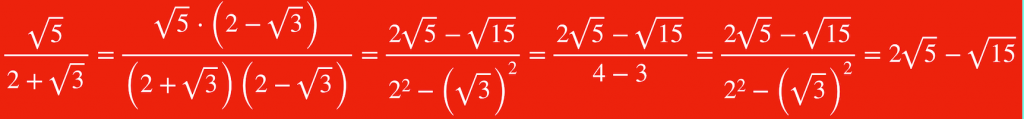
Segundo ejemplo:

Cuando en el denominador hay una suma y los dos sumandos son raíces cuadradas. (También vale si en el denominador aparece una resta)

El conjugado solo es cambiar el signo a la expresión:

√b+√c su conjugado es √b-√c

FÍJATE QUE SE MULTIPLICA EL NUMERADOR Y EL DENOMINADOR POR EL CONJUGADO. EN CASO CONTRARIO ESTARÍA MAL

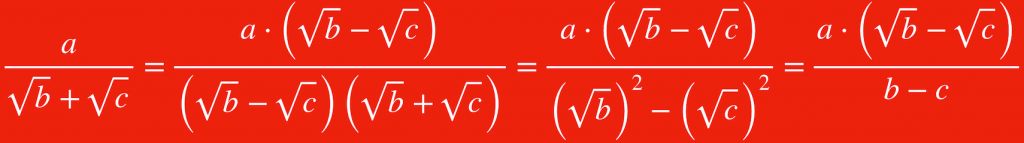
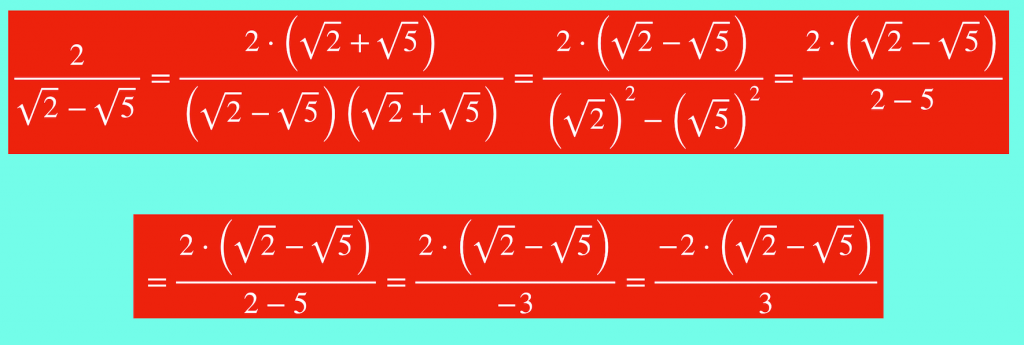
EJERCICIOS RACIONALIZAR

En este apartado vas a ver ejercicios de racionalización para 3º ESO, 4º ESO Y 1º de Bachillerato. Tanto si eres estudiante como profesor tienes unos pdfs que te van a ayudar.

Aquí tienes ejercicios para racionalizar de 1º de bachillerato en pdf

Estos son ejercicios para racionalizar de 3º de ESO en pdf

Y también ejercicios de racionalización de radicales de 4º de ESO en pdf

EJERCICIOS RESUELTOS DE RADICALES. EJERCICIOS RESUELTOS DE RACIONALIZACIÓN

Aquí tienes las soluciones a los ejercicios de racionalización anteriores y paso a paso

$\small \frac{1}{\sqrt{7}}=\frac{\sqrt{7}}{\sqrt{7}\cdot \sqrt{7}}=\frac{\sqrt{7}}{\left (\sqrt{7}\right )^2}=\frac{\sqrt{7}}{7}\newline \frac{6}{\sqrt{2}}=\frac{6\sqrt{2}}{\sqrt{2}\cdot \sqrt{2}}=\frac{6\sqrt{2}}{\left (\sqrt{2}\right )^2}=\frac{6\sqrt{2}}{2}=\newline 3\sqrt{2}\newline \frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{3}\cdot \sqrt{2}}{\sqrt{2}\cdot \sqrt{2}}=\frac{\sqrt{6}}{\left (\sqrt{2}\right )^2}=\frac{\sqrt{6}}{2} \newline \frac{9\sqrt{5}}{\sqrt{6}}=\frac{9\sqrt{5}\cdot \sqrt{6}}{\sqrt{6}\cdot \sqrt{6}}=\frac{9\sqrt{30}}{\left (\sqrt{6}\right )^2}=\frac{9\sqrt{30}}{6}=\frac{3\sqrt{30}}{2} \newline$

MÁS EJERCICIOS DE RACIONALIZAR

$\small \frac{3}{\sqrt[3]{4^2}}=\frac{3\sqrt[3]{4}}{\sqrt[3]{4^2}\cdot \sqrt[3]{4}}=\frac{3\sqrt[3]{4}}{\sqrt[3]{4^3}}=\frac{3\sqrt[3]{4}}{4}\newline \frac{12}{\sqrt[7]{3^5}}=\frac{12\sqrt[7]{3^2}}{\sqrt[7]{3^5}\cdot \sqrt[7]{3^2}}=\frac{12\sqrt[7]{3^2}}{\sqrt[7]{3^7}}=\frac{12\sqrt[7]{3^2}}{3}=4\sqrt[7]{3^2}\newline \frac{2}{\sqrt[5]{6}}=\frac{2\sqrt[5]{6^4}}{\sqrt[5]{6}\cdot \sqrt[5]{6^4}}=\frac{2\sqrt[5]{6^4}}{\sqrt[5]{6^5}}=\frac{2\sqrt[5]{6^4}}{6}=\frac{\sqrt[5]{6^4}}{3}\newline \frac{7}{\sqrt[4]{5^2}}=\frac{7\sqrt[4]{5^2}}{\sqrt[4]{5^2}\cdot \sqrt[4]{5^2}}=\frac{7\sqrt[4]{5^2}}{\sqrt[4]{5^4}}=\frac{7\sqrt[4]{5^2}}{5}$

Y OTROS POQUITOS MÁS

$\dpi{100} \small \frac{\sqrt{6}+\sqrt{3}}{\sqrt{6}-\sqrt{3}}=\frac{\left (\sqrt{6}+\sqrt{3} \right )\cdot \left (\sqrt{6}+\sqrt{3} \right )}{\left (\sqrt{6}-\sqrt{3} \right )\cdot \left (\sqrt{6}+\sqrt{3} \right )}=\newline=\frac{\left (\sqrt{6}+\sqrt{3} \right )^2}{\left (\sqrt{6}\right )^2-\left (\sqrt{3} \right )^2}=\frac{\left (\sqrt{6}\right)^2+\left (\sqrt{3} \right )^2+2\cdot \sqrt{6}\cdot \sqrt{3}}{6-3}=\newline=\frac{6+3+2\sqrt{18}}{3}=\frac{9+2\sqrt{18}}{3}=\newline=\frac{9+2\cdot 3\sqrt{2}}{3}=3+2\sqrt{2}\newline$

$\tiny \frac{\sqrt{x+y}+\sqrt{x-y}}{\sqrt{x+y}-\sqrt{x-y}}=\frac{\left ( \sqrt{x+y}+\sqrt{x-y} \right )\cdot \left ( \sqrt{x+y}+\sqrt{x-y} \right )}{\left ( \sqrt{x+y}-\sqrt{x-y} \right )\cdot \left ( \sqrt{x+y}+\sqrt{x-y} \right )}=\newline=\frac{\left ( \sqrt{x+y}+\sqrt{x-y} \right )^2}{\left (\sqrt{x+y}\right )^2-\left ( \sqrt{x-y} \right )^2}=\frac{\left ( \sqrt{x+y}\right )^2+\left ( \sqrt{x-y} \right )^2+2\cdot \sqrt{x+y}\cdot \sqrt{x-y}}{x+y-x+y}=\newline=\frac{x+y+x-y+2\sqrt{\left ( x+y \right )\left ( x-y \right )}}{2y}=\frac{2x+2\sqrt{x^2-y^2}}{2y}=\frac{x+\sqrt{x^2-y^2}}{y}\newline$

$\small \frac{1+\sqrt{2}}{1-\sqrt{2}}=\frac{\left (1+\sqrt{2} \right )\cdot \left ( 1+\sqrt{2} \right )}{\left (1-\sqrt{2} \right )\cdot \left (1+\sqrt{2} \right )}=\newline=\frac{\left (1+\sqrt{2} \right )^2}{1^2-\left ( \sqrt{2} \right )^2}=\frac{1^2+\left ( \sqrt{2}\right )^2+2\cdot 1\cdot \sqrt{2}}{1-2}=\newline=\frac{1+2+2\sqrt{2}}{-1}=-3-2\sqrt{2}$

$\small \frac{5}{1-\sqrt{2}}+\frac{3}{1+\sqrt{2}}=\frac{5\left (1+\sqrt{2} \right )}{\left (1- \sqrt{2} \right)\cdot \left (1+\sqrt{2} \right )}+\newline+\frac{3\left (1-\sqrt{2} \right )}{\left (1+\sqrt{2}\right )\cdot \left (1- \sqrt{2} \right )}=\newline=\frac{5+5\sqrt{2}}{1^2-\left ( \sqrt{2} \right )^2}+\frac{3-3\sqrt{2}}{1^2-\left ( \sqrt{2} \right )^2}=\newline=\frac{5+5\sqrt{2}}{-1}+\frac{3-3\sqrt{2}}{-1}=\newline=-5-5\sqrt{2}-3+3\sqrt{2}=-8-2\sqrt{2}$

$\small \frac{1}{\sqrt[4]{8}}=\frac{\sqrt[4]{8^3}}{\sqrt[4]{8}\cdot \sqrt[4]{8^3}}=\frac{\sqrt[4]{8^3}}{\sqrt[4]{8^4}}=\newline=\frac{\sqrt[4]{8^3}}{8}=\frac{\sqrt[4]{\left ( 2^3 \right )^3}}{8}=\frac{\sqrt[4]{2^9}}{8}=\frac{2^2\sqrt[4]{2}}{8}=\newline=\frac{\sqrt[4]{2}}{2}$

Y OTROS MÁS DIFÍCLES

$\small \frac{12\sqrt{2}}{\sqrt{6}-\sqrt{2}}=\frac{12\sqrt{2}\left ( \sqrt{6}+\sqrt{2} \right )}{\left (\sqrt{6}-\sqrt{2} \right )\left ( \sqrt{6}+\sqrt{2} \right )}=\newline=\frac{12\sqrt{12}+12\sqrt{4}}{\left (\sqrt{6}\right)^2-\left (\sqrt{2} \right )^2}=\frac{12\sqrt{2^2\cdot 3}+12\cdot 2}{6-2}=\newline=\frac{12\cdot 2\sqrt{3}+24}{4}=\frac{24\sqrt{3}+24}{4}=6\sqrt{3}+6$

$\small \frac{-3}{2\sqrt{3}-3}=\frac{-3\left (2\sqrt{3}+3\right )}{\left (2\sqrt{3}-3 \right )\left ( 2\sqrt{3}+3 \right )}=\newline=\frac{-6\sqrt{3}-9}{\left (2\sqrt{3}\right)^2-3^2}=\frac{-6\sqrt{3}-9}{4\cdot 3-9}=\newline=\frac{-6\sqrt{3}-9}{12-9}=\frac{-6\sqrt{3}-9}{3}=-2\sqrt{3}-3$

$\small \frac{7}{\sqrt{7}\sqrt[3]{3}}=\frac{7\sqrt{7}\sqrt[3]{3^2}}{\sqrt{7}\sqrt{7}\sqrt[3]{3}\sqrt[3]{3^2}}=\newline=\frac{7\sqrt{7}\sqrt[3]{3^2}}{\left ( \sqrt{7} \right )^2\sqrt[3]{3^3}}=\frac{7\sqrt{7}\sqrt[3]{3^2}}{7\cdot 3}=\frac{\sqrt{7}\sqrt[3]{3^2}}{3}$

$\small \frac{1+\sqrt{7}}{2\sqrt{7}+5}=\frac{\left (1+\sqrt{7} \right )\cdot \left ( 2\sqrt{7}-5 \right )}{\left (2\sqrt{7}+5 \right )\cdot \left (2\sqrt{7}-5 \right )}=\newline=\frac{2\cdot7-5\sqrt{7}+2\sqrt{7}-5}{\left ( 2\sqrt{7} \right )^2-5^2}=\newline=\frac{14-3\sqrt{7}-5}{4\cdot 7-25}=\frac{9-3\sqrt{7}}{3}=3-\sqrt{7}$

$\small \frac{3\sqrt{2}}{4\sqrt{3}-3\sqrt{2}}-\left (\sqrt{6}-2\right)^2=\frac{3\sqrt{2}\left ( 4\sqrt{3}+3\sqrt{2} \right )}{\left ( 4\sqrt{3}-3\sqrt{2} \right )\left ( 4\sqrt{3}+3\sqrt{2} \right )}-\newline-\left (\sqrt{6}-2\right)^2=\frac{12\sqrt{6}+9\cdot 2}{\left ( 4\sqrt{3}\right )^2-\left (3\sqrt{2} \right )^2}-\left(\sqrt{6}\right)^2-4+2\cdot 2\sqrt{6}=\newline=\frac{12\sqrt{6}+18}{16\cdot 3-9\cdot 2}-6-4+4\sqrt{6}=\newline=\frac{12\sqrt{6}+18}{48-18}-10+4\sqrt{6}=\frac{12\sqrt{6}+18}{30}-10+4\sqrt{6}=\newline=\frac{2\sqrt{6}+3}{5}-10+4\sqrt{6}=\newline=\frac{2\sqrt{6}+3-50+20\sqrt{6}}{5}=\frac{22\sqrt{6}-47}{5}$

$\small \frac{\sqrt{5}}{2\sqrt{5}-4}+\frac{5}{2\sqrt{5}}=\frac{\sqrt{5}\left ( 2\sqrt{5}+4 \right )}{\left ( 2\sqrt{5}-4 \right ) \left ( 2\sqrt{5}+4 \right )}+\newline+\frac{5\sqrt{5}}{2\sqrt{5}\sqrt{5}}=\frac{10+4\sqrt{5}}{\left ( 2\sqrt{5}\right)^2-4^2}+\frac{\sqrt{5}}{2}=\newline=\frac{20+8\sqrt{5}+\sqrt{5}}{4}=\frac{20+9\sqrt{5}}{4}$

canal de youtube sobre matemáticas, @masmath

¡Descubre las matemáticas en nuestro canal de YouTube! 🌟 Aprende trucos, resuelve problemas paso a paso y domina conceptos clave con nuestros vídeos fáciles de seguir. 🚀 Haz clic aquí y empieza a disfrutar de las matemáticas de forma sencilla y divertida. ¡Te esperamos! 🎓📚

EJERCICIOS DE RACIONALIZACIÓN RESUELTOS CON SOLUCIONES

Racionalización ejercicios resueltos pdf. Aquí tienes un nuevo pdf con los ejercicios y sus soluciones para que compruebes tus ejercicios de racionalizar.

SOLO TIENES QUE HACER CLIC AQUÍ Y ACCEDERAS AL pdf TOTALMENTE GRATIS

Pues aquí tienes otro pdf para descargar con todas las soluciones. ejercicios de racionalización 4 eso resueltos pdf

Dicho esto, propiedades como tal, no las hay. Lo que hay son casos y cada uno de ellos tiene la forma de resolverlos, FÍJATE CÓMO LOS RESUELVO.

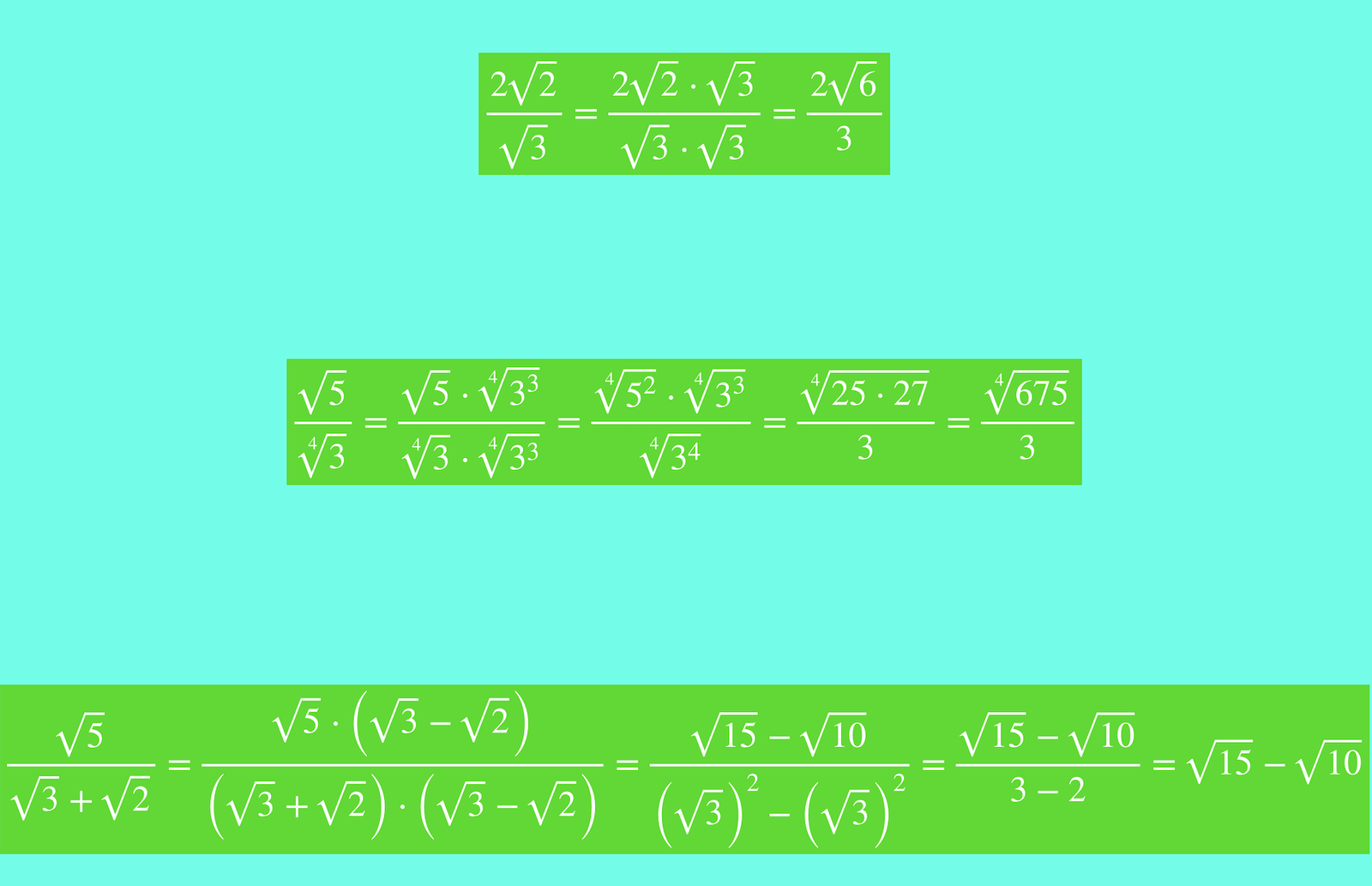
Te voy a explicar paso a paso estos tres ejercicios sobre racionalizar denominadores, en concreto hay tres casos:

PRIMER CASO: ¿cómo sacar la raíz cuadrada del denominador?

En este caso vas a aprender a resolver ejercicios de racionalización cuando en el denominador solo hay factores con raíces cuadradas, ¿y por qué factores? Mira estos casos y entenderás lo que te digo:

Fíjate en el primer ejemplo que te voy a explicar:

Al tener en el denominador una raíz cuadrada tienes que multiplicar y dividir por el mismo denominador y obtener una fracción equivalente donde en el denominador y gracias al producto de radicales se elimina la raíz, que es tú objetivo:

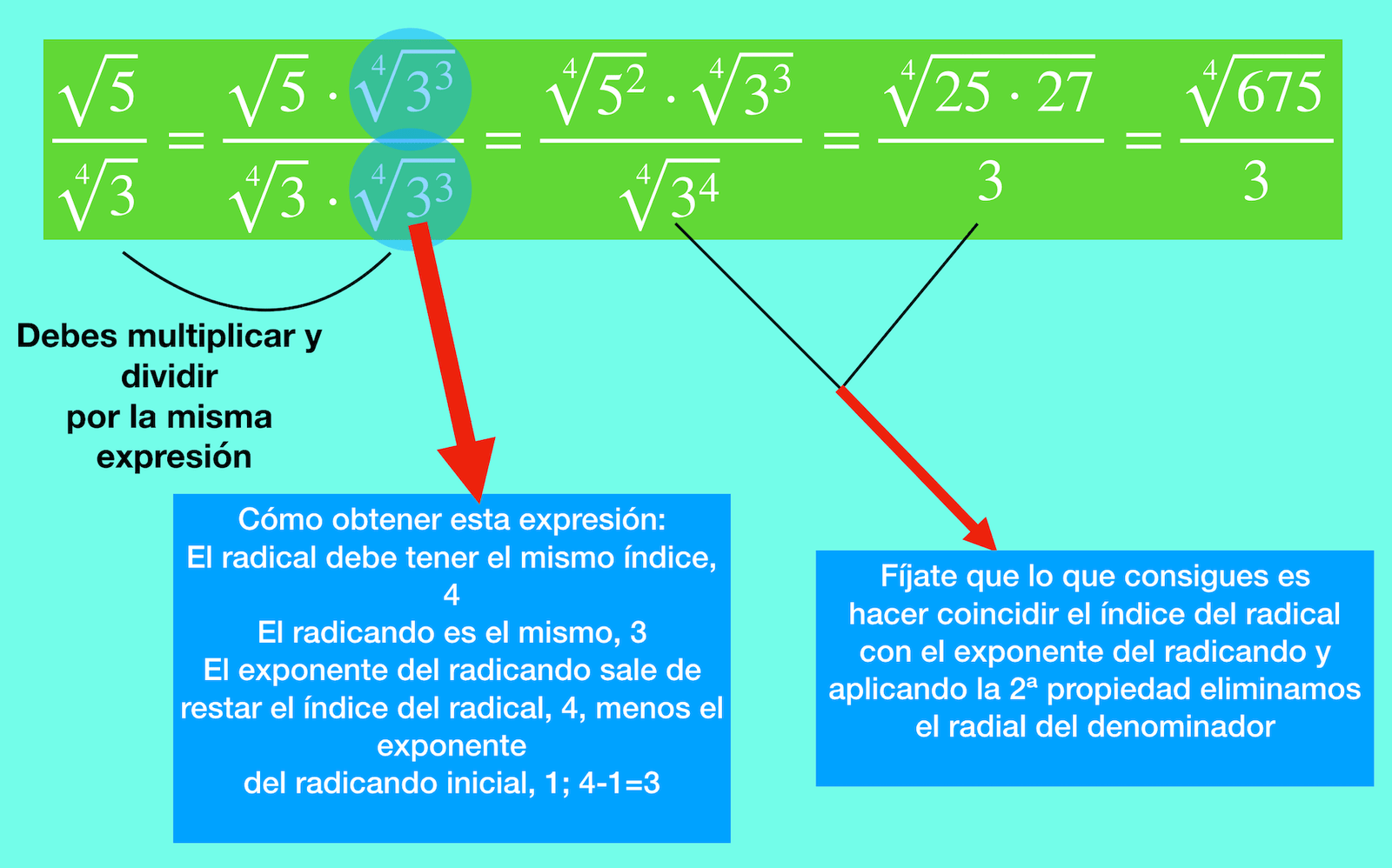
SEGUNDO CASO: ¿qué hacer cuando hay una raíz en el denominador? ➤ no cuadrada

¿Qué ocurre cuándo te encuentras con raíces en el denominador que no sean de índice cuadrado? te explico, debes tener en cuenta estas dos propiedades de los radicales:

$\sqrt[n]{a^{x}}\cdot \sqrt[n]{a^{y}}=\sqrt[n]{a^{x+y}}$
$\sqrt[n]{a^{n}}=a$

¿Cómo las vas a utilizar? mira, fíjate bien vas a hacer este ejemplo conmigo:

$\frac{^{\sqrt{5}}}{\sqrt[4]{3}}$

Como puedes comprobar, en el denominador, hay una única raíz de índice 4. Tu objetivo es eliminar esa raíz del denominador. Aquí lo que debes multiplicar, tanto el numerador como el denominador, por una raíz del mismo índice y cuyo radicando sea igual elevado al exponente resultante de restar el índice del radical del denominador menos el exponente del radicando.

😿

Ja, ja, ja, te explico con este ejemplo. Oye que la teoría está bien, pero te la voy a explicar:

TERCER CASO: ¿cómo se racionaliza un binomio?

Este caso es especial y debes prestar mucha atención. Si te has dado cuenta en los dos casos anteriores lo que he hecho es multiplicar y dividir la fracción por una expresión común para conseguir el objetivo de eliminar el denominador.

En esta racionalización también lo haremos así, ¿cuál es la expresión? bueno, para poder racionalizar dos raíces que se están sumando en el denominador y además son cuadradas debemos de multiplicar y dividir por el conjugado de la expresión.

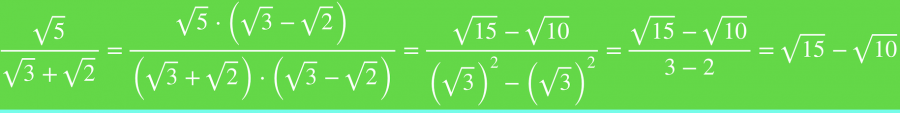
CONCLUSIÓN

La racionalización de denominadores es un proceso fundamental en el estudio de las matemáticas, especialmente en niveles como 4º de ESO. A través de ejercicios resueltos y ejemplos de racionalización de radicales, los estudiantes pueden entender de manera práctica cómo simplificar expresiones que involucran raíces. Para facilitar el aprendizaje, es recomendable descargar ejercicios de racionalización en PDF, donde se pueden encontrar distintos casos de racionalización con soluciones detalladas. Si estás buscando más material, muchos recursos en línea ofrecen la oportunidad de racionalizar denominadores con ejercicios variados y resolver las dudas más comunes que suelen surgir. Además, los ejercicios resueltos ayudan a consolidar el conocimiento en temas avanzados de álgebra y radicales.

TE PUEDE INTERESAR:

ANÁLISIS MATEMÁTICO

DERIVADAS

INTERVALOS